EN中文

热带地理 >

2024 , Vol. 44 >Issue 6: 1036 - 1046

DOI: https://doi.org/10.13284/j.cnki.rddl.20230928

台风致灾因子模拟分析

基于C-Vine Copula函数的台风灾害链“风-雨-潮”联合概率分布研究

  • 周子滢 , 1, 2, 3 ,
  • 杨赛霓 , 1, 2 ,
  • 刘晓燕 4 ,
  • 唐继婷 5 ,
  • 石永国 6, 7
展开
  • 1. 北京师范大学 教育部巨灾模拟与系统性风险应对国际合作联合实验室，广东 珠海 519087
  • 2. 北京师范大学 国家安全与应急管理 学院，广东 珠海 519087
  • 3. 北京师范大学 系统科学学院，北京 100875
  • 4. 北京师范大学 环境演变与自然灾害教育部重点实验室，北京 100875
  • 5. 中国矿业大学（北京） 人工智能学院，北京 100083
  • 6. 浙江省应急管理科学研究院，杭州 311121
  • 7. 浙江省安全工程与技术研究重点实验室，杭州 311121
杨赛霓（1975—），女，江苏常州人，博士，教授，主要研究方向为风险评估管理，（E-mail）。

周子滢（1999—），女，江苏苏州人，硕士研究生，主要研究方向为沿海灾害风险评估，（E-mail）；

收稿日期: 2023-11-30

  修回日期: 2024-01-24

  网络出版日期: 2024-06-13

基金资助

浙江科技厅领雁项目(2022C03107)

收起

Joint Probability Distribution of Typhoon Disaster Chain "Strong Wind-Rainstorm- Storm Surge" Based on C-Vine Copula Function

  • Ziying Zhou , 1, 2, 3 ,
  • Saini Yang , 1, 2 ,
  • Xiaoyan Liu 4 ,
  • Jiting Tang 5 ,
  • Yongguo Shi 6, 7
Expand
  • 1. Joint International Research Laboratory of Catastrophe Simulation and Systemic Risk Governance, Beijing Normal University, Zhuhai 519087, China
  • 2. School of National Safety and Emergency Management, Beijing Normal University, Zhuhai 519087, China
  • 3. School of Systems Science, Beijing Normal University, Beijing 100875, China
  • 4. Key Laboratory of Environmental Change and Natural Disasters, Ministry of Education, Beijing Normal University, Beijing 100875, China
  • 5. School of Artificial Intelligence, China University of Mining and Technology-Beijing, Beijing 100083, China
  • 6. Zhejiang Academy of Emergency Management Science, Hangzhou 311121, China
  • 7. Zhejiang Key Laboratory of Safety Engineering and Technology, Hangzhou 311121, China

Received date: 2023-11-30

  Revised date: 2024-01-24

  Online published: 2024-06-13

Fold

摘要

现有台风灾害链研究大多采用高维对称Copula模型建立多个致灾因子的联合分布，对致灾因子之间非线性、非对称的复杂关联结构探究不足。文章以浙江岛屿城市舟山为例，通过C-Vine Copula函数刻画当地台风灾害链“风-雨-潮”之间的复杂依赖关系，利用1979—2018年逐日的最大持续风速、累积降雨量以及最大风暴增水数据估算三者的联合概率分布以及重现期。研究表明：1）风速与降雨量在常规数值区间（非极端情况）具有较强的相关性，最佳联合分布为Frank Copula；风速与风暴增水具有上尾依赖的特征，最佳联合分布为Gumbel Copula；2）降雨量分布在风速条件下显示2处峰值，风暴增水分布在风速条件下近似于均匀，两者之间的最佳联合分布为Gumbel Copula；3）以单变量100 a重现期为例，风速-降雨量与风速-风暴增水组合事件的二维联合重现期分别缩短至29和30 a，而风速-降雨量-风暴增水组合事件的三维联合重现期缩短至17 a。综上，C-Vine Copula函数能准确有效地刻画台风灾害链“风-雨-潮”之间的复杂依赖关系，深化对于台风灾害链内在作用机制的理解，为台风灾害风险管理和工程设计提供科学支持。

关键词： 台风; 灾害链; 联合概率分布; Copula函数; C-Vine; 舟山市

本文引用格式

周子滢 , 杨赛霓 , 刘晓燕 , 唐继婷 , 石永国 . 基于C-Vine Copula函数的台风灾害链“风-雨-潮”联合概率分布研究[J]. 热带地理, 2024 , 44(6) : 1036 -1046 . DOI: 10.13284/j.cnki.rddl.20230928

Abstract

Typhoons and their associated disaster chains pose serious threats to the lives and property of coastal residents, and they remain a focal point for research and response. Previous studies on typhoon disaster chains often employed high-dimensional symmetric Copula models to establish the joint distribution of multiple hazard factors, however they failed to explore the complex nonlinear and asymmetric dependencies among them. This study aimed to depict these complex relationships more comprehensively and efficiently to provide a more accurate typhoon hazard assessment. Focusing on Zhoushan, a city comprising numerous islands in Zhejiang Province that faces multiple typhoon threats, this study employed the C-Vine Copula function to model the complex dependencies among "strong wind-rainstorm-storm surge" in the typhoon disaster chain. Utilizing observational data from 1979 to 2018, this study involves three main steps: first, fitting the marginal distribution of each hazard factor and identifying the best one from Lognormal, Gamma, GEV (Generalized Extreme Value), and Burr functions based on the K-S test; second, fitting the bivariate joint distributions of wind speed-rainfall and wind speed-storm surge using Gaussian, Clayton, Gumbel, Frank, and Joe Copula functions, and determining the best fit based on the AIC (Akaike Information Criterion); and finally, estimating the trivariate joint probability distribution and corresponding return periods for wind speed-rainfall-storm surge using the C-Vine Copula function. This revealed (1) a strong correlation between wind speed and rainfall observed within regular value ranges (non-extreme conditions), were best represented by the Frank Copula, In addition, wind speed and storm surge exhibit an upper-tail dependence, best captured by the Gumbel Copula. (2) The rainfall distribution under certain wind speed conditions revealed dual peaks, whereas the storm surge distribution maintained a uniform pattern, with the best joint distribution fitting the Gumbel Copula. (3) Considering a 100-year return period for individual variables, the bivariate return periods for wind speed-rainfall and wind speed-storm surge events were significantly reduced to 29 and 30 years, respectively, while the trivariate return period for the wind speed-rainfall-storm surge combination was further reduced to 17 years. Overall, the C-Vine Copula function effectively characterizes the complex nonlinear and asymmetric dependencies among the typhoon disaster chain "strong wind-rainstorm-storm surge", reducing high-dimensional parameter estimation complexity. This method provides new insights for constructing joint probability and return period models for multiple hazard factors and offers a scientific basis for disaster risk assessment and management strategies. Therefore, this enhances the accuracy of disaster prevention and mitigation efforts. Additionally, the application of the C-Vine Copula assists to deeply understand the mechanisms and development processes of natural disasters, providing new tools for on-site emergency response and decision-making.

Key words： typhoon; disaster chain; joint probability distribution; Copula function; C-Vine; Zhoushan City

全球范围内，台风因其巨大的破坏性而备受关注（Meiler et al., 2022）。尤其是台风灾害链“大风-暴雨-风暴潮”的复合危险性，对人类社会和自然环境构成重大威胁（王静爱 等，2012；王然 等，2016）。中国拥有超过3.2万km的海岸线，是受到台风影响最为严重的国家之一（Bloemendaal et al., 2022）。根据《中国气象灾害年鉴》（中国气象局，2021），2003—2020年全国因台风累计遭受直接经济损失9 541.2亿元。在这些受影响地区中，岛屿城市因其前线位置和单一生态而对台风灾害尤为脆弱，此外，岛屿城市面临着大风、暴雨、风暴潮等致灾因子的多重威胁。因此，针对岛屿城市开展台风“风-雨-潮”的联合概率分析，不仅有助于理解灾害链的动态变化和互作机制，而且对于制定有效的灾害预防和减缓措施具有重要价值。
Copula函数不受边缘分布函数的限制，能通过变量之间的相关结构，灵活地构建多个变量的联合分布函数（Sklar, 1959）。目前，Copula函数已经在水文（武传号 等，2014；卢韦伟 等，2015；宋松柏 等，2018；何兵 等，2019）、气象（曹伟华 等，2016；张野 等，2017；于忱 等，2018；黄宇 等，2022）等领域的联合概率分析中发挥重要作用。然而，在台风灾害的研究中，关注点大多集中在风雨（侯静惟 等，2019；Tang et al., 2022；刘青 等，2022）、雨潮（Xu et al., 2018；许瀚卿 等，2022）、风潮（王灶平 等，2014；闫长城 等，2016）等双致灾因子的联合概率分析。虽然已有研究尝试采用高维对称Copula函数分析多个台风致灾因子的联合分布，如许红师等（2018）使用三维Gumbel Copula函数分析台风引起的风速、暴雨和潮位的联合分布以及失效概率；贺芳芳等（2021）基于三维Copula联合函数的超越概率模型，计算“雨洪风”“雨洪潮”和“雨风潮”3种“三碰头”联合超越概率。但这些传统方法大多采用单一参数或者单一依赖结构来刻画多维变量的联合分布，无法灵活地建模非线性和非对称关系，尤其是在涉及“风-雨-潮”复杂的依赖关系时，可能导致联合重现期估计不准确。
Vine Copula函数能将多维依赖结构分解为一系列二维Copula函数，通过层级结构为多变量建模（Bedford and Cooke, 2001; 2002）。相较于传统的高维Copula函数，Vine Copula可以灵活地选择Copula函数来建模不同变量间的依赖关系。如对于下尾依赖的成对变量可以使用Clayton Copula，对于上尾依赖的成对变量可以使用Gumbel Copula。这种方法不仅能更准确地捕捉变量之间的非线性、非对称依赖关系，而且显著降低了高维参数估计的复杂度（曾文颖 等，2022；白晓宇，2022；周晓 等，2023）。考虑到在台风过程中“风”为核心驱动因素，本研究创新性地选用C-Vine Copula函数构建“风-雨-潮”之间的依赖结构，旨在深化对台风灾害链内在作用机制的理解。选择浙江省舟山市为案例，该地区作为东海沿岸的关键门户，海岸线绵延曲折，常年遭受台风侵袭，面临多重灾害影响。本研究综合考虑台风引发的大风、暴雨和风暴潮3个致灾因子，基于舟山市1979—2018年逐日最大持续风速、累积降雨量以及最大风暴增水，使用C-Vine Copula函数计算它们的联合概率分布和重现期。这不仅为当地防风抗洪工程提供了更加科学的设计标准，而且为灾害风险评估和管理策略制定提供了新的视角和方法。

1 数据与方法

1.1　研究区域与数据

舟山市位于中国东海沿岸，由众多岛屿组成，总面积达1 440 km2。该地区属于亚热带季风气候区，夏秋两季经常受到台风侵袭，面临大风、暴雨和风暴潮等致灾因子的多重威胁。如2021年第6号强台风“烟花”和2022年第12号强台风“梅花”，这2场台风均于浙江舟山沿海登陆，并引发“风雨潮”三碰头的极端灾害性事件，在当地造成巨大的经济损失和社会影响（闵惠学 等，2023；叶舟 等，2023）。
本研究使用1979—2018年逐日的最大持续风速、累积降雨量（24 h）以及最大风暴增水数据分析风雨潮联合概率分布。为确保研究的可重复性、可再现性以及可扩展性，本研究获取资料均为全球范围内长期、连续、标准化的数据集，且公开免费获取。其中，最大持续风速和累积降雨量来自全球逐日气象站点数据集GSOD（Global Surface Summary of the Day），在舟山市区范围内只有定海站1个气象站（表1），能提供1956年至今逐日的基本气象要素数据。最大风暴增水来自于全球潮汐和风暴潮再分析数据集GTSR （Global Tide and Surge Reanalysis）（Muis et al., 2016; 2020），沿着舟山海岸线有多个潮位站点，选择距离气象站最近的潮位站（见表1）匹配，能提供1979—2018年逐日的最大风暴增水数据。天文潮汐作为潮位的主要成分，极大地受到月球引力影响，为排除其干扰，本研究没有直接采用实际潮位观测数据，而选择风暴增水再分析数据进行“风-雨-潮”联合概率分析。
表1 基本数据说明

Table 1 Basic data description

站点 编号 经度（°E） 纬度（°N） 数据来源 要素 时间分辨率 时间范围
气象站 584770 122.117 30.033 全球逐日气象站点数据集GSOD 最大持续风速 逐日 1956年至今
累积降雨量（24 h）
潮位站 16461 122.183 30.103 全球潮汐和风暴潮再分析数据集GTSR 最大风暴增水 逐日 1979―2018年
根据已有经验（许红师 等，2018；Yang and Qian, 2019; Shi et al., 2021; Tang et al., 2022），本研究定义以舟山市定海站潮位站为中心的500 km缓冲区作为潜在影响范围，基于中国气象局热带气旋最佳路径数据集筛选出该范围内的台风记录，并提取出台风影响当日的风速、降水量和风暴增水数据。为了确保数据分析的准确性和一致性，剔除3个要素中任意一个存在缺失值的记录。

1.2　研究方法

1.2.1　二维Copula 函数及边缘分布函数

Copula函数可以表示多个随机变量之间的关联结构，且不受边缘分布的限制。根据Sklar定理，如果 X 1 , X 2 , … , X n是 n个连续随机变量，那么存在一个Copula函数 C，能够描述相应的联合累积分布函数（Sklar, 1959）：
         F X 1 , … , X n = C F 1 X 1 , F 2 X 2 , … , F n X n
式中 : F X 1 , … , X n是 X 1 , … , X n的联合累积分布函数； F 1 X 1 , F 2 X 2 , … , F n X n是 X 1 , … , X n的边缘分布函数； C是Copula函数。
Copula函数种类繁多，其中椭圆类Copula和阿基米德Copula最为常用。本研究从中选取Gaussian、Clayton、Gumbel、Frank以及Joe五种Copula函数形式刻画二维变量联合概率分布，相应公式见表2所示（Salvadori et al., 2016），并通过AIC准则确定最优函数。对于风、雨、潮三者的边缘函数分布，分别采用对数正态分布（Lognormal）、伽马分布（Gamma）、广义极值分布（GEV）以及伯尔分布（Burr）4种函数形式进行拟合，并通过K-S检验确定最优分布函数。
表2 常用的二维Copula函数公式

Table 2 Formulas of common two-dimensional Copula functions

函数名称 累积概率分布公式 参数 θ范围 参数 θ与参数 τ的换算关系
Gaussian C   ( u , v ) = Φ θ Φ - 1 ( u ) ,   Φ - 1 ( v ) 0 ≤ θ ≤ 1 τ = 2 π a r c s i n   ( θ )
Clayton C ( u , v ) = m a x u - θ + v - θ - 1 ,   0 - 1 / θ θ > 0 τ = θ θ + 2
Gumbel C ( u , v ) = e x p - ( - l o g   u ) θ + ( - l o g   v ) θ 1 / θ θ ≥ 1 τ = 1 - 1 θ
Frank C ( u , v ) = - 1 θ l o g   1 + e - θ u - 1 e - θ v - 1 e - θ - 1 θ ≠ 0 τ = 1 - 4 θ + 4 θ ∫ 0 θ x / θ e x - 1 d x
Joe C ( u , v ) = 1 - ( 1 - u ) θ + ( 1 - v ) θ - ( 1 - u ) θ ( 1 - v ) θ 1 / θ θ ≥ 1 τ = 1 + 4 θ 2 ∫ 0 1 x l o g ( x ) ( 1 - x ) 2 ( 1 - θ ) / θ d x

注：变量 u , v分别表示成对台风致灾因子的累积概率； C   ( u , v )表示相应的联合累积概率； θ表示Copula函数关联参数； τ表示Kendall秩相关系数； Φ表示正态分布函数。

1.2.2　C-Vine Copula函数

Vine Copula函数，是Copula函数的一种高级扩展形式，采用 n n - 1 / 2个二维双变量或条件二维Copula函数的级联来创建 n维多变量分布。与传统Copula函数相比，Vine Copula函数能捕捉高维变量间更加复杂的非线性和非对称依赖关系，同时显著降低高维参数估计的复杂度。其中，C-Vine（C藤）作为Vine Copula的一种特定结构，特别适用于存在一个或多个核心驱动变量的情境，能有效处理核心变量与其他变量间复杂的依赖关系（Jalili and Najafi, 2022）。
考虑到台风过程中风对雨和潮的主导作用，本研究构建了一个以风速 w为中心，降雨量 r和风暴增水 s为分支的C-Vine树形结构。如图1-a所示，首先在第一层树（T1）中创建二维Copula函数 C w , r和 C w , s，代表风速 w和降雨量 r以及风速 w和风暴增水 s之间的依赖关系；然后在第二层树（T2）中创建条件二维Copula函数 C r , s | w，代表风速-降雨量 w , r和风速-风暴增水 w , s之间的依赖关系。如图1-b所示，通过 C w , r将风速累积概率函数 F w与降雨量累积分布函数 F r相连结，即可推求风速-降雨联合概率函数 F w , r；通过 C w , s将风速累积分布函数 F w与风暴增水累积概率函数 F s相连结，即可推求风速-风暴增水联合分布函数 F w , s；通过 C r , s | w将风速-降雨联合概率函数 F w , r与风速-风暴增水联合概率函数 F w , s相连结，即可推求风速-降雨量-风暴增水联合概率函数 F w , r , s。
图1 以风为核心的风雨潮C-Vine结构

Fig.1 Wind-centered C-vine structure based on wind speed, rainfall, and storm surge

因此，基于C-Vine copula函数的风雨潮联合累积函数 F w , r , s可表示为：
F w , r , s = F w × C R , S W C R | W r | w , C S | W s | w     
式中： w , r , s分别表示风速、降雨量以及风暴增水； F ( w )是风速的累积概率函数； C R | W , C S | W分别表示给定风速条件下降雨量、风暴增水的条件概率函数； C R , S W表示 C R | W和   C S | W之间的二维Copula函数。
根据条件概率定理，对于 C R | W , C S | W有：
     C R | W r | w = P ( r ≤ R w ≤ W ) = P r ≤ R , w ≤ W P w ≤ W = C W , R w , r F w
     C S | W s | w = P ( s ≤ S w ≤ W ) = P s ≤ S , w ≤ W P w ≤ W = C W , S w , s F w
式中： C W , R w , r表示风速-降雨量的Copula函数； C W , S w , s表示风速-风暴增水的Copula函数。

1.2.3　联合重现期

重现期指某一特定事件（ x ≥ X）在给定时间间隔 N内发生1次的平均时间长度。单变量重现期 T u n i可表示为：
T u n i = N n × 1 - F x X
式中： N为观测样本时间长度； n为观测时段内变量 x超越给定阈值 X出现的次数。
进一步地，联合重现期是指多个特定事件（ x ≥ X , y ≥ Y , ⋯）在给定时间间隔 N内至少发生1次的平均时间长度。因此，双变量联合重现期 T b i和三变量联合重现期 T t r i可表示为：
T b i = N n × 1 - C F x X , F y Y
T t r i = N n × 1 - C F x X , F y Y , F z Z
式中： F x X 、 F y Y 、 F z Z分别表示变量 x 、 y 、 z的累积概率； C为Copula函数； C F x X , F y Y表示双变量 x , y的联合累积概率； C F x X , F y Y , F z Z表示三变量 x 、 y 、 z的联合累积概率。

2 结果分析

2.1　风、雨、潮边缘概率分布

采用对数正态分布、伽马分布、广义极值分布以及伯尔分布分别拟合舟山市风雨潮3个致灾因子的边缘分布，并使用K-S检验评价各分布函数的拟合效果（表3）。其中，D值为样本分布与参考分布差异的度量，P值为差异显著性的度量，D值越小，P值越大，拟合效果越好。由表3可知，风速的最优分布为对数正态分布（D值=0.102，P值=0.011），降雨量的最优分布为为伯尔分布（D值=0.043，P值=0.721），风暴增水的最优分布为也同样为伯尔分布（D值=0.037，P值=0.865），三者均通过0.01显著性检验，其最优边缘分布函数及其对应参数见表4。此外，伽马分布也适用于降雨量的分布拟合，而广义极值分布也适用于风暴增水的分布拟合，拟合效果仅次于最优的伯尔分布，P值均通过0.01显著性检验。
表3 风速、降雨量和风暴增水的边缘分布K-S检验

Table 3 K-S test for the marginal distributions of wind speed, rainfall, and storm surge

变量 对数正态分布 伽马分布 广义极值分布 伯尔分布
D值 P值 D值 P值 D值 P值 D值 P值
风速/（m ∙s-1） 0.102 0.011 0.106 0.007 0.104 0.008 0.107 0.006
降雨量/mm 0.082 0.065 0.058 0.366 0.093 0.025 0.043 0.721
风暴增水/m 0.049 0.572 0.061 0.295 0.039 0.824 0.037 0.865

注：加粗之处表示拟合最优分布函数所对应的D值和P值。

表4 风速、降雨量和风暴增水的最优边缘分布及其对应参数

Table 4 Optimal marginal distributions for wind speed, rainfall, and storm surge and their corresponding parameters

变量 边缘分布 参数值
风速（ w）/（m ∙s-1） F w ; μ w , σ w = 1 2 1 + e r f l n w - μ w σ w 2 μ w = 0.314 , σ w = 0.481  
降雨量（ r）/mm F r ; c r , d r , μ r , σ r = 1 - 1 + r - μ r σ r - c r - d r c r = 2.046 ,   d r = 0.253   μ r = 0.253 ,   σ r = 54.799
风暴增水（ s）/m F s ; c s , d s , μ s , σ s = 1 - 1 + r - μ s σ s - c s - d s c s = 3.068 ,   d s = 1.646   μ s = 0.003 ,   σ s =   0.317
图2显示风速、降雨量和风暴增水的累积概率分布情况。其中，风速累积概率曲线呈现“S”型，在0~2 m/s区间缓慢上升，在2~10 m/s区间快速跃升，在10~20 m/s区间增速放缓，而在20~30 m/s区间趋于平缓，表明台风事件中风速出现极端低值或极端高值的情况较为罕见，多数情况集中在10~20 m/s左右。与此相对的，降雨量累积概率曲线呈现上“C”型，在0~15 mm低值区间快速攀升，随后增速放缓。与风速相比，降雨量在高值区间没有显现明显的“平台”，表现出一定的长尾效应。风暴增水累积概率曲线变化与风速相似，在1.25~1.50 m高值区间呈现边际效应。这些累积概率曲线对于理解不同灾害因素的频率和强度分布至关重要，并且在进行灾害链风险评估时，上述分布特征有助于横向分析不同要素之间的相互关系。
图2 风速、降雨量和风暴增水的累积概率分布

Fig.2 Cumulative probability distribution of wind speed, rainfall, and storm surge

2.2　风-雨和风-潮联合概率分布

分别采用Gaussian、Clayton、Gumbel、Frank和Joe五种Copula函数描述风速-降雨量以及风速-风暴增水的二维联合分布，并计算相应的AIC值。一般来说，AIC值越小，Copula函数的拟合效果越好。由表5可知，风速-降雨量对应的最优函数为Frank Coupla（Kendall相关系数 τ = 0.34，关联参数 θ = 3.45），而风速-风暴增水对应的最优函数为Gumbel Copula（Kendall相关系数 τ = 0.28，关联参数 θ = 1.38）。根据最优Copula函数的依赖特性可知，风速和降雨量无明显的尾部依赖特征，在常规数值区间（非极端情况）具有较强的相关性；而风速和风暴增水具有上尾依赖的特性，即在极端高值区间具有较强的相关性。
表5 风速-降雨量、风速-风暴增水二维联合分布

Table 5 Two-dimensional joint distribution of wind speed-rainfall and wind speed-storm surge

Copula函数 风速-降雨量 风速-风暴增水
θ τ AIC θ τ AIC
Gaussian 0.38 0.25 -59.64 0.43 0.28 -48.33
Clayton 0.10 0.05 -14.90 0.36 0.15 -15.53
Gumbel 1.15 0.13 -18.42 1.38 0.28 -54.23
Frank 3.45 0.34 -71.95 2.78 0.29 -47.66
Joe 1.06 0.03 -5.09 1.58 0.25 -53.43

注：加粗之处表示拟合最优Copula函数所对应的参数 θ、参数 τ和AIC值。

风速-降雨量（图3-a）和风速-风暴增水（图3-b）的二维联合概率分布展示了不同变量组合下的联合概率分布值。当风速为10 m/s，降雨量为50 mm，风暴增水为0.5 m时，对应风速-降雨量以及风速-风暴增水的联合累积概率均为0.58，表明超过半数台风事件引起的是低强度风雨潮灾害。此外，风速累积概率为0.75，降雨量累积概率为0.81，风暴增水累积概率为0.68，表明三者在累积分布中具有非同步性，降雨量相比风暴增水，在温和风速下倾向于低值。而当风速为20 m/s，降雨量为100 mm，风暴增水为1.0 m时，对应的风速-降雨量和风速-风暴增水的联合累积概率分别为0.92和0.96，表明极端情况下容易出现风雨潮的联合。此外，风速累积概率为0.98，降雨量累积概率为0.94，风暴增水累积概率为0.95，表明风速与风暴增水的累积概率在高值区间具有更好的同步性。
图3 风速-降雨量（a）和风速-风暴增水（b）二维联合概率分布

Fig.3 Two-dimensional joint distribution of wind speed-rainfall (a) and wind speed-storm surge (b)

2.3　风-雨-潮联合概率分布

根据条件概率定理，降雨量和风暴增水在特定风速下的条件概率，为风速-降雨量、风速-风暴增水联合概率与相应风速概率之比的微分。图4显示了特定风速下降雨量和风暴增水的条件概率分布。其中，降雨量在风速条件下的直方图（红色）在0.18和0.93附近出现峰值，表明这2个区间所对应的风速能够促进水汽凝结抬升形成降雨；而风暴增水在风速条件下的直方图（蓝色）则近似于均匀分布，频率不随风速条件变化而发生明显改变，意味着风暴增水可能更多受到地形等其他因素的影响。此外，降雨量与风暴增水在风速条件下的散点图（灰色）在“高-高”和“低-低”区域出现微弱的集聚现象，表明降雨量和风暴增水存在一定的正相关性。
图4 降雨量和风暴增水在特定风速下的条件概率分布

Fig.4 Conditional distribution of rainfall and storm surge under specific wind speed conditions

进一步地，分别采用Gaussian、Clayton、Gumbel、Frank和Joe五种Copula函数描述降雨量和风暴增水2个条件概率之间的依赖关系。如表6所示，通过最小化AIC原则确定出两者的最优分布为Gumbel Copula（Kendall相关系数 τ = 0.16，关联参数 θ = 1.19）。将风速-降雨量和风速-风暴增水的联合累积概率分布代入，得到风速-降雨量-风暴增水联合累积概率分布（图5）。随着风速、降雨量和风暴增水的增加，三者的联合概率分布值增大。为更加直观地展示，绘制了风速累积概率为0.2（ w ≤ 4.9   m / s）、0.4（ w ≤ 6.5   m / s）、0.6（ w ≤ 8.2   m / s）以及0.8（ w ≤ 10.7   m / s）4种情况下降雨量-风暴增水的联合累积概率分布（图6），可知，随着风速的增加，概率分布倾向于较高的降雨量和风暴增水，表明高强度的风速对于高强度的降雨量和风暴增水具有诱发性，这种认识对于预测和应对极端天气事件有重要启示。
表6 降雨量和风暴增水在风速条件下的二维联合分布

Table 6 Two-dimensional joint distribution of rainfall and storm surge under wind speed conditions

Copula函数 降雨量-风暴增水
θ τ AIC
Gaussian 0.18 0.11 -11.00
Clayton 0.02 0.01 1.27
Gumbel 1.19 0.16 -17.68
Frank 1.65 0.18 -17.52
Joe 1.29 0.14 -16.85

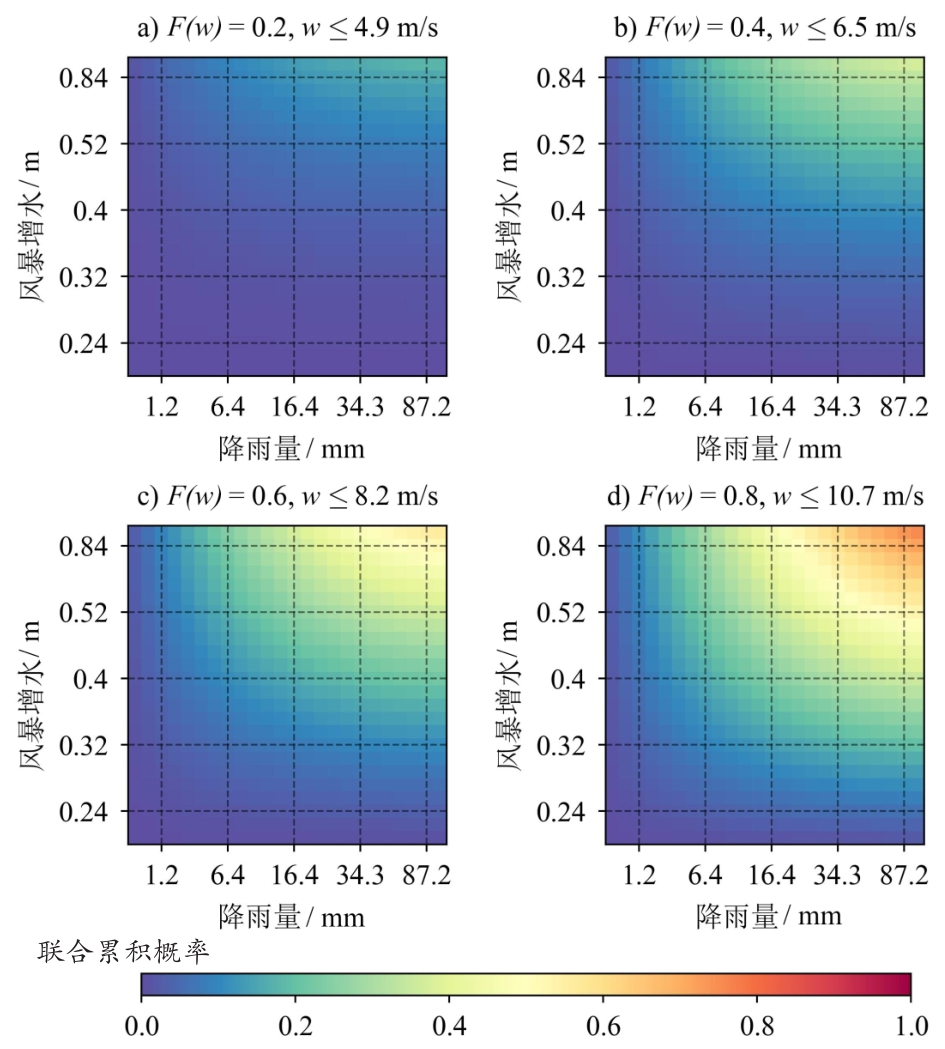
注：加粗数值表示拟合最优Copula函数所对应的参数 θ、参数 τ和AIC值。

图5 风速-降雨量-风暴增水的联合累积概率分布

Fig.5 Joint cumulative distribution of wind speed, rainfall, and storm surge

图6 特定风速条件下降雨量-风暴增水的联合概率分布

Fig.6 Joint distribution of rainfall and storm surge under specific wind speed conditions

2.4　联合重现期计算

根据重现期定义，计算得到风雨潮单变量重现期、二维联合重现期以及三维联合重现期（表7）。随着重现期的增加，相应风速、降雨量和风暴增水的数值均有增加。其中，降雨量从5 a重现期水平的50.29 mm，到100 a重现期水平的134.76 mm，呈现明显的长尾效应。对于同一水平的风速、降雨量以及风暴增水，三维联合重现期始终小于二维联合重现期，也小于单变量重现期。以单变量100 a重现期为例，风速-降雨量组合事件与风速-风暴增水组合事件的联合重现期分别为28.74和29.67 a，而风速-降雨量-风暴增水组合事件的联合重现期仅为17.14 a。以上结果强调在综合考虑风速、降雨量和风暴增水3个变量时，对于灾害风险的评估更具现实意义。因此，在台风灾害风险管理和工程设计中，计算灾害链多致灾因子的联合影响十分必要。
表7 风速-降雨量-风暴增水单变量重现期、二维联合重现期及三维联合重现期

Table 7 Univariate, two-dimensional, and three-dimensional return period of wind speed, rainfall, and storm surge

重现期/a 风速/（m ∙s-1） 降雨量/mm

风暴

增水/m

 联合重现期/a
T b i ( w , r ) T b i ( w , s ) T t r i ( w , r , s )
5 11.08 50.29 0.62 1.73 2.09 1.2
10 12.51 67.2 0.72 3.17 3.87 2.13
20 13.84 85.1 0.82 6.19 7.75 4.19
50 15.66 114.1 0.98 16.18 19.31 10.07
100 16.76 134.76 1.09 28.74 29.67 17.14

2.5　C-Vine Copula与三维对称Copula的比较

为突出C-Vine Copula在建模“风-雨-潮”复杂依赖关系方面的优势，将其与三维对称Copula函数（包括Gaussian、Clayton、Gumbel、Frank以及Joe）的拟合结果进行比较（表8）。一般来说，AIC值越小，对数似然函数值越大，则模型拟合效果越好。结果表明，C-Vine Copula函数能更准确有效地刻画台风灾害链“风-雨-潮”之间复杂的非线性、非对称依赖关系。
表8 C-Vine Copula与三维对称Copula的比较

Table 8 Comparison between C-Vine Copula and Three-Dimensional Symmetric Copula

Copula函数 参数值 AIC值 对数似然函数值
Gaussian 0.354 -117.696 59.848
Clayton 0.094 -23.136 12.568
Gumbel 1.357 -142.811 72.405
Frank 2.796 -138.500 70.250
Joe 1.562 -134.994 68.497
C-Vine — -143.859 74.930

注：加粗数值表示拟合最优Copula函数所对应的参数值、AIC值和对数似然函数值。

3 结论与讨论

本研究以岛屿城市舟山为例，综合考虑台风引发的大风、暴雨和风暴潮3个致灾因子，采用C-Vine Copula函数构建台风灾害链“风-雨-潮”之间的依赖关系，从而估算三者的联合概率分布以及重现期，得到的主要结论为：
1）风速、降雨量和风暴增水对应的最优边缘分布函数分别为对数正态分布（风速）和伯尔分布（降雨量和风暴增水），拟合结果均通过0.01显著性水平检验，具有较高的置信度。其中，风速累积概率曲线呈现“S”型分布，在高值区间出现明显的“平台”；降雨量累积概率曲线呈现上“C”型分布，表现出一定的长尾效应；而风暴增水与风速相似，在高值区域呈现边际效应。
2）风速-降雨量的最佳联合概率分布为Frank Copula，表明风速和降雨量在常规数值区间（非极端情况）具有较强的相关性；风速-风暴增水的最佳联合概率分布为Gumbel Copula，反映风速和风暴增水具有上尾依赖的特征，即在极值情况下依赖性将会增强。风速、降雨量和风暴增水三者的累积分布在高值区间呈现较好的同步性，表明超强台风事件下容易出现风雨潮的联合。
3）降雨量分布在风速条件下显示2个峰值，相应区间风速能促进水汽凝结抬升形成降雨；而风暴增水分布在风速条件下近似于均匀，频率不随着风速条件而产生明显变化，意味着风暴增水可能更多受到其他因素的影响。降雨量-风暴增水的最佳联合概率分布为Gumbel Copula，也反映上尾依赖特征。
4）对于同一水平的风速、降雨量和风暴增水，三维联合重现期始终小于二维联合重现期和单变量重现期。以单变量100 a重现期为例，风速-降雨量组合事件与风速-风暴增水组合事件的联合重现期分别缩短至29和30 a，而风速-降雨量-风暴增水组合事件的联合重现期缩短至17 a。这表明极端条件下大风、暴雨和风暴潮联合出现的频率可能远高于通常预期，因此在实际的风险管理和工程设计中需综合考虑多个致灾因子的联合和链式效应。
总的来说，C-Vine Copula函数能有效刻画台风灾害链“风-雨-潮”之间复杂的非线性、非对称依赖关系，降低高维参数估计难度。该方法提供构建多元致灾因子联合概率和重现期模型的新思路，为灾害风险评估和管理策略制定提供科学依据，从而增强防灾减灾工作的准确性。此外，应用C-Vine Copula还有助于深入洞察自然灾害的形成机理和发展过程，为实地应急、响应和决策提供新的工具。
本研究的主要不足之处在于，主要依赖于站点观测数据，可能无法完全捕捉到更广泛或罕见的台风灾害事件。为了克服这一限制，未来研究可以结合卫星遥感、雷达监测和地面观测等多源数据，这将有助于进一步提高模型的空间分辨率，并增强对复杂灾害事件的评估能力。此外，未来还需考虑气候变化的影响，分析气候变暖背景下台风灾害链的可能变化趋势。

脚注

周子滢：完成整体研究设计和论文撰写；

杨赛霓：提供研究思路并指导论文撰写；

刘晓燕：参与数据收集处理与分析；

唐继婷：提供研究工具和方法；

石永国：帮助审阅和修订论文。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
白晓宇. 2022. 近海风浪地震组合概率特性及跨海桥梁致灾机理与易损性评估方法. 北京：北京交通大学.

Bai Xiaoyu. 2022. Combination Probability Characteristic of Coastal Wind, Wave, and Earthquake and the Disaster-Causing Mechanism and Vulnerability Assessment Method of Sea-Crossing Bridge. Beijing: Beijing Jiaotong University.

Bedford T and Cooke R M. 2001. Probability Density Decomposition for Conditionally Dependent Random Variables Modeled by Vines. Annals of Mathematics and Artificial Intelligence, 32: 245-268.

Bedford T and Cooke R M. 2002. Vines-A New Graphical Model for Dependent Random Variables. The Annals of Statistics, 30(4): 1031-1068.

Bloemendaal N, De Moel H, Martinez A B, Muis S, Haigh I D, Van Der Wiel K, Haarsma R J, Ward P J, Roberts M J, Dullaart J C M, and Aerts J C J H. 2022. A Globally Consistent Local-Scale Assessment of Future Tropical Cyclone Risk. Science Advances, 8(17): eabm8438.

曹伟华，梁旭东，赵晗萍，段小刚，张自银. 2016. 基于Copula函数的北京强降水频率及危险性分析. 气象学报，74（5）：772-783.

Cao Weihua, Liang Xudong, Zhao Hanping, Duan Xiaogang, and Zhang Ziyin. 2016. Copula Based Frequency Analysis and Its Application in Hazard Risk Assessment of Heavy Rainfall in Beijing. Acla Meteorologica Sinica, 74(5): 772-783.

曾文颖，徐明庆，宋松柏，吴昊昊. 2022. 基于R-Vine Copula函数的极端降水联合分布模型及风险识别. 水资源保护，38（6）：96-103.

Zeng Wenying, Xu Mingqing, Song Songbai, and Wu Haohao. 2022. Joint Probability Distribution and Risk Identification of Extreme Precipitation Based on R-Vine Copula Function. Water Resources Protection, 38(6): 96-103.

何兵，高凡，唐小雨，覃姗. 2019. 基于滑动Copula函数的新疆干旱内陆河流水文气象要素变异关系诊断. 水土保持研究，26（1）：155-161.

He Bing, Gao Fan, Tang Xiaoyu, and Qin Shan. 2019. Diagnosis of Variation of the Relationship between Hydrological and Meteorological Elements in Arid Inland Rivers of Xinjiang Based on the Sliding Copula Function. Research of Soil and Water Conservation, 26(1): 155-161.

贺芳芳，梁卓然，董广涛. 2021. 上海地区洪涝致灾因子复合概率及未来变化分析. 灾害学，36（2）：9-13.

He Fangfang, Liang Zhuoran, and Dong Guangtao. 2021. Analysis on the Compound Probability and Future Change of Flood and Waterloging Disaster Factors in Shanghai. Journal of Calastrophology, 36(2): 9-13.

侯静惟，方伟华，程锰，叶妍婷，吴鹏，韩轶男. 2019. 基于Copula函数的海南热带气旋风雨联合概率特征分析. 自然灾害学报，28（3）：54-64.

Hou Jingwei, Fang Weihua, Cheng Meng, Ye Yanting, Wu Peng, and Han Yinan. 2019. Joint Probability Analysis of Tropical Cyclone Wind and Rainfall for Integrated Hazard Severity Assessment in Hainan. Journal of Natural Disasters, 28(3): 54-64.

黄宇，张冰哲，庞慧珍，徐璟，刘磊，王彪. 2022. 基于混合Copula优化算法的风速预测方法研究. 太阳能学报，43（10）：192-201.

Huang Yu, Zhang Bingzhe, Pang Huizhen, Xu Jing, Liu Lei, and Wang Biao. 2022. Research on Wind Speed Forecasting Method Based on Hybrid Copula Optimization Algorithm. Acta Energiae Solaris Sinica, 43(10): 192-201.

Jalili Pirani F and Najafi M R. 2022. Multivariate Analysis of Compound Flood Hazard Across Canada's Atlantic, Pacific and Great Lakes Coastal Areas. Earth's Future, 10(8): e2022EF002655.

刘青，王军，许瀚卿，牛怡莹，魏旭辰. 2022. 台风影响下沿海城市风雨复合灾害风险研究——以海口市为例. 灾害学，37（4）：129-134.

Liu Qing, Wang Jun, Xu Hanqing, Niu Yiying, and Wei Xuchen. 2022. Research on the Risk of Joint Wind and Rain Hazards in Coastal Cities During Typhoons: A Case Study of Haikou City. Journal of Calastrophology, 37(4): 129-134.

卢韦伟，陈璐，周建中，陈华. 2015. 基于多元分布函数的区域洪水频率分析. 水文，35（5）：6-10.

Lu Weiwei, Chen Lu, Zhou Jianzhong, and Chen Hua. 2015. Regional Flood Frequency Analysis Based on Multivariate Distribution Function. Journal of Hydrology, 35(5): 6-10.

Meiler S, Vogt T, Bloemendaal N, Ciullo A, Lee C Y, Camargo S J, Emanuel K, and Bresch D N. 2022. Intercomparison of Regional Loss Estimates from Global Synthetic Tropical Cyclone Models. Nature Communications, 13(1): 6156.

闵惠学，许波刘，陈金浩. 2023. 浙江省“2022·12”号台风潮雨洪等综合分析//《中国防汛抗旱》杂志社,水利部防洪抗旱减灾工程技术研究中心（水旱灾害防御中心）. 2022—2023年度全国典型洪旱过程应对技术经验交流会论文集. 杭州：浙江省水文管理中心，90-94.

Min Huixue, Xu Boliu, and Chen Jinhao. 2023. Comprehensive Analysis of Typhoon, Storm Surge, and Floods in Zhejiang Province during "2022·12". In: China Flood and Drought Management, Research Center on Flood & Drought Disaster Prevention and Reduction of the Ministry of Water Resources. Proceedings of the National Symposium on Response Techniques and Experiences for Typical Flood and Drought Processes 2022-2023. Hangzhou: Zhejiang Provincial Hydrology Bureau, 90-94.

Muis S, Verlaan M, Winsemius H C, Aerts J C J H, and Ward P J. 2016. A Global Reanalysis of Storm Surges and Extreme Sea Levels. Nature Communications, 7(1): 11969.

Muis S, Apecechea M I, Dullaart J, De Lima Rego J, Madsen K S, Su J, Yan K, and Verlaan M. 2020. A High-Resolution Global Dataset of Extreme Sea Levels, Tides, and Storm Surges, Including Future Projections. Frontiers in Marine Science, 7: 263.

Shi X, Chen B, Liang Y, Zhang B, and Ye T. 2021. Inundation Simulation of Different Return Periods of Storm Surge Based on a Numerical Model and Observational Data. Stochastic Environmental Research and Risk Assessment, 35(10): 2093-2103. DOI:10.1007/s00477-021-02010-3.

Sklar M. 1959. Fonctions de Répartition à n Dimensions et Leurs Marges. Annales de l'Institut Statistique de l'Université de Paris, 8(3): 229-231.

Salvadori G, Durante F, De Michele C, Bernardi M, and Petrella L. 2016. A Multivariate Copula‐Based Framework for Dealing with Hazard Scenarios and Failure Probabilities. Water Resources Research, 52(5): 3701-3721.

宋松柏，王小军. 2018. 基于Copula函数的水文随机变量和概率分布计算. 水利学报，49（6）：687-693.

Song Songbai and Wang Xiaojun. 2018. Probability Distribution Calculation of the Sum of Hydrological Random Variables Based on Copula Function Approach. Journal of Hydraulic Engineering, 49(6): 687-693.

Tang J, Hu F, Liu Y, Wang W, and Yang S. 2022. High-Resolution Hazard Assessment for Tropical Cyclone-Induced Wind and Precipitation: An Analytical Framework and Application. Sustainability, 14(21): 13969.

王静爱，雷永登，周洪建，尹衍雨，常晟，李群芳. 2012. 中国东南沿海台风灾害链区域规律与适应对策研究. 北京师范大学学报（社会科学版），1（2）：130-138.

Wang Jing'ai, Lei Yongdeng, Zhou Hongjian, Yin Yanyu, Chang Sheng, and Li Qunfang. 2012. Regional Features and Adaptation Countermeasures of Typhoon Disaster Chains in Southeast Coastal Regions of China. Journal of Beijing Normal University(Social Sciences), 1(2): 130-138.

王然，连芳，余瀚，史培军，王静爱. 2016. 基于孕灾环境的全球台风灾害链分类与区域特征分析. 地理研究，35（5）：836-850.

Wang Ran, Lian Fang, Yu Han, Shi Peijun, and Wang Jing'ai. 2016. Classification and Regional Features Analysis of Global Typhoon Disaster Chains Based on Hazard-Formative Environment. Geographical Research, 35(5): 836-850.

王灶平，刘桂平，龚政，张长宽. 2014. 考虑风、潮联合概率分布的海堤超越频率分析. 水利水电科技进展，34（6）：18-22.

Wang Zaoping, Liu Guiping, Gong Zheng, and Zhang Changkuan. 2014. Exceeding Cumulative Probability Analysis of Seawall Considering the Joint Probability Distribution of Tide Level and Wind Speed. Advances in Science and Technology of Water Resources, 34(6): 18-22.

武传号，黄国如，吴思远. 2014. 基于Copula函数的广州市短历时暴雨与潮位组合风险分析. 水力发电学报，33（2）：33-40.

Wu Chuanhao, Huang Guoru, and Wu Siyuan. 2014. Risk Analysis of Combinations of Short Duration Rainstorm and Tidal Level in Guangzhou Based on Copula Function. Journal of Hydroelectric Engineering, 33(2): 33-40.

许瀚卿，谭金凯，李梦雅，王军. 2022. 基于Copula函数的沿海城市雨潮复合灾害风险研究. 自然灾害学报，31（1）：40-48.

Xu Hanqing, Tan Jinkai, Li Mengya, and Wang Jun. 2022. Compound Flood Risk of Rainfall and Storm Surge in Coastal Cities Based on Copula Formal. Journal of Natural Disasters, 31(1): 40-48.

许红师，练继建，宾零陵，徐奎. 2018. 台风灾害多元致灾因子联合分布研究. 地理科学，38（12）：2118-2124.

Xu Hongshi, Lian Jijian, Bin Lingling, and Xu Kui. 2018. Joint Distribution of Multiple Typhoon Hazard Factors. Scientia Geographica Sinica, 38(12): 2118-2124.

Xu H, Xu K, Bin L, Lian J, and Ma C. 2018. Joint Risk of Rainfall and Storm Surges during Typhoons in a Coastal City of Haidian Island, China. International Journal of Environmental Research and Public Health, 15(7): 1377.

闫长城，刘耀辉. 2016. 基于风潮联合概率分布的海堤设防标准分析. 水利规划与设计，（10）：20-22.

Yan Changcheng and Liu Yaohui. 2016. Analysis of Coastal Embankment Design Standards Based on Wind-Tide Joint Probability Distribution. Water Resources Planning and Design, (10): 20-22.

Yang X, and Qian J. 2019. Joint Occurrence Probability Analysis of Typhoon-Induced Storm Surges and Rainstorms Using Trivariate Archimedean Copulas. Ocean Engineering, 171: 533-539.

叶舟，顾文炜，陈芳. 2023. 舟山相关海域台风暴潮增水研究. 水运工程，（12）：8-15，21.

Ye Zhou, Gu Wenwei, and Chen Fang. 2023. Study on the Typhoon Storm Surge Increase in the Waters around Zhoushan. Port & Waterway Engineering, (12): 8-15, 21.

于忱，陈隽，王红瑞，朱中凡，来文立. 2018. 多变量Copula函数在干旱风险分析中的应用进展. 南水北调与水利科技，16（1）：14-21.

Yu Chen, Chen Jun, Wang Hongrui, Zhu Zhongfan, and Lai Wenli. 2018. Application Progress of Multi-Variate Copula Function in Drought Risk Analysis. South-to-North Water Transfers and Water Science & Technology, 16(1): 14-21.

张野，王康，刘欣铭，张苏辰，周嘉，王菜林. 2017. 基于Copula函数的暴雨要素三维联合分布——以宽甸县为例，地理科学，37（4）：603-610.

Zhang Ye, Wang Kang, Liu Xinming, Zhang Suchen, Zhou Jia, and Wang Cailin. 2017. The Three-Dimensional Joint Distributions of Rainstorm Factors Based on Copula Function: A Case in Kuandian County, Liaoning Province. Scientia Geographica Sinica, 37(4): 603-610.

中国气象局. 2021. 中国气象灾害年鉴 （2020）. 北京：气象出版社.

China Meteorological Administration. 2021. Yearbook of Meteorological Disasters in China (2020). Beijing: China Meteorological Press.

周晓，吴瑞雅，郭泽勇，梁巧倩，杨朝晖，李昭春. 2023. 基于C-Vine-Copula函数的暴雨致灾危险性联合分布研究. 气象与环境科学，46（5）：104-111.

Zhou Xiao, Wu Ruiya, Guo Zeyong, Liang Qiaoqian, Yang Zhaohui, and Li Zhaochun. 2023. Study on the Joint Distribution of Rainstorm Disaster Risk Based on C-Vine-Copula Function. Meteorological and Environmental Sciences, 46(5): 104-111.

Options
文章导航

/

〈 〉